Creative Coding with Circles
This article was originally published here.
Right around the beginning of May, in the last few days of April, I began learning OpenRNDR. As a way to learn the framework, the first things I tried to code were circles. And lots of them! I coded circles in such profundity as I’ve never had in my life.
With that impulse, I found myself coding every single day and most of the work I produced involved circles. I would like to share what I found with you!
Trails
By varying the size and the position of the circle, then drawing it as it moves, taking care not to erase its path, the outcome is something that resembles pulled candy. The animation at the beginning of the article was created using this technique.

You can always store previous positions in an array and then continue to vary the size and color as new circles get drawn. You end up with something funkier!

Another technique is to have multiple trails being drawn at the same time. In the animation above, it looks like the camera is panning, following the pulsing circles. But it actually isn’t!
The circles calculates its size based on the size of the circle above it. In other words, the radii of the circles are propagated down the circle stack. It’s a technique that artist Zach Lieberman — who I absolutely revere — uses. By doing so, you don’t end up with a gigantic array of circles and only have to deal with a finite number of circles.
Soddy Circles
Please don’t ask me who coined the term Soddy Circles. But let me explain it anyways. Given three mutually tangent circles — that is, three circles touching each other — a soddy circle is a circle that is tangent to all three circles at the same time.
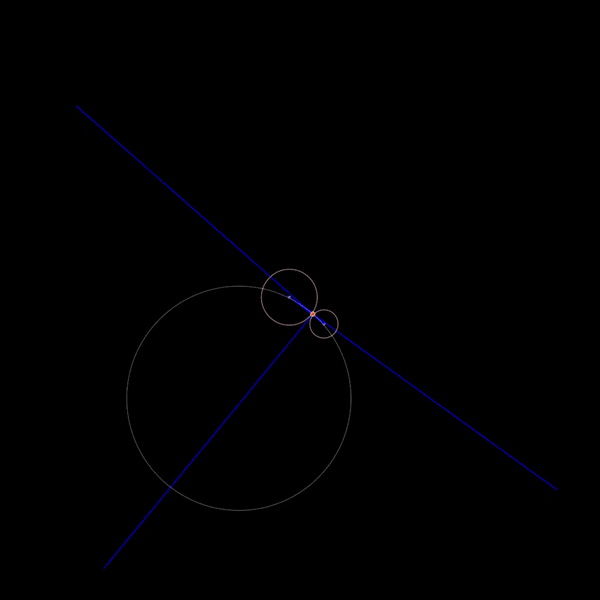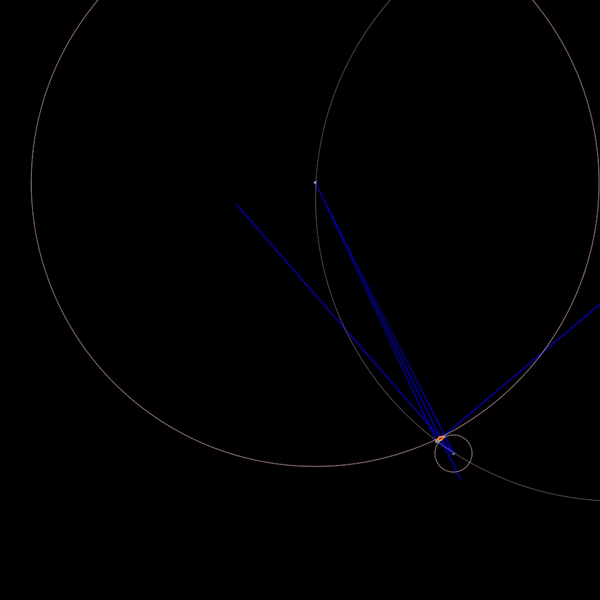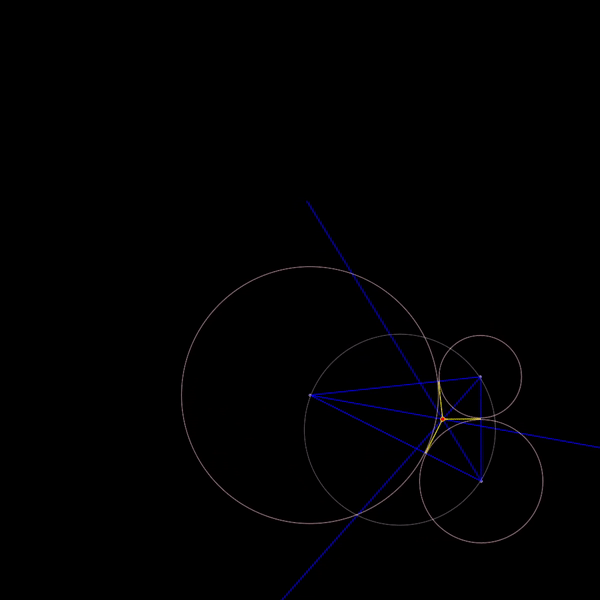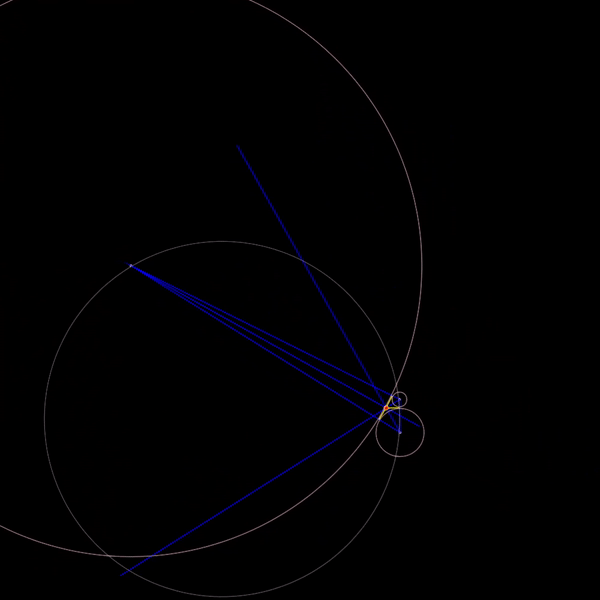
The construction of soddy circles begins with the construction of three mutually tangent circles! Given three arbitrary points, you can always construct three circles such that they are mutually tangent and where they don’t contain one another.
There are a algebraic methods to solve this problem, but since my math is bad, I opted for the geometric method. The blue lines you see above are the intermediate construction geometries that you need to first draw in order to find the solution.
Working on this problem felt like I was back in primary school, with a compass, ruler and a piece of paper, working out what I could and couldn’t draw.
With that problem solved, it’s now time to find the soddy circles! You could read up about it before hand, but in trying to solve this, I discovered a property about soddy circles that freaked me out. It turns out, given the constraints, you could always find an inner soddy circle. In fact, the previous geometric constructions help you find it!

However, there isn’t a clear formula for finding the outer soddy circle. Logically, I thought that if there could always be an inner circle, then there should always be an outer circle! But this assumption is wrong.
While there can always be a larger circle mutually tangent to all three, there are times where it overlaps and thus negates the solution. Finding this out was pretty neat but it wasn’t really artistic…yet.
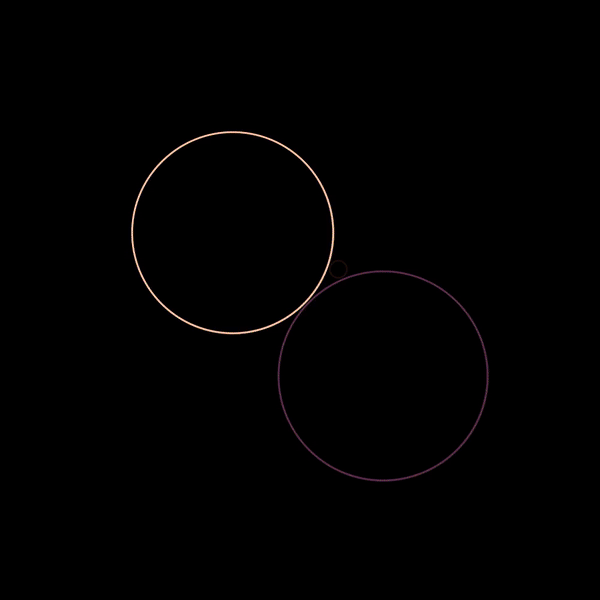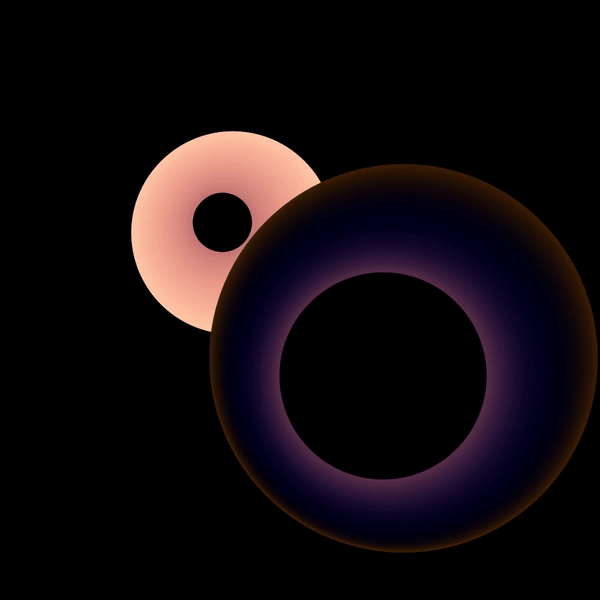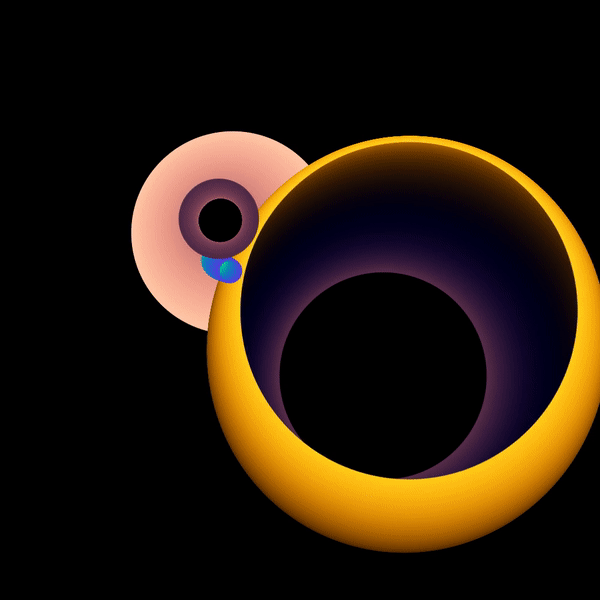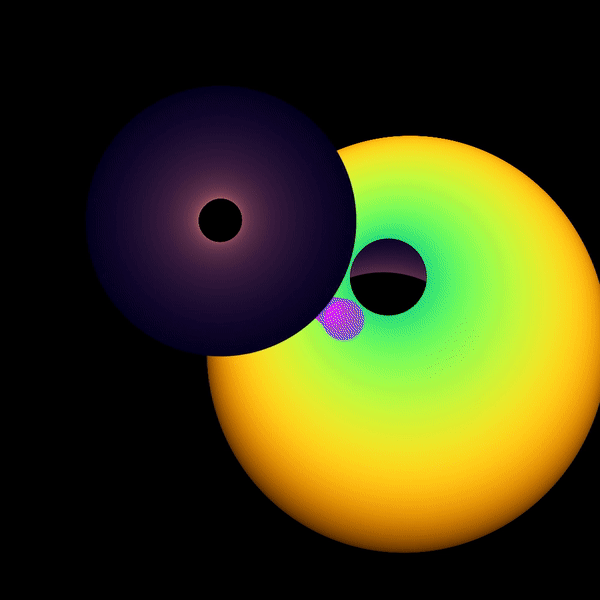
It starts to look better with a little color and a trailing effect! The trailing effect is the very same technique as the one mentioned in this article.

Adding some transparency and shortening the trails as new ones are drawn gives
a more interesting result.

And lastly, I added some interaction. If you’d like to play with it, click here!
Trees
One technique I explored with circles was the idea of trees. I formulated the problem this way:
- Start out with a circle in the center
- Spawn a circle that doesn’t intersect or contain another existing circle
- Repeat until the screen is filled

I animated this to solve one step of the problem per frame and coded up my own tree structure to store the relationships. Every time a circle is spawned, it stores a reference to the circle it is tangent to and vice versa.

Varying the size gives you patterns with different qualities. Drawing the lines between the circles shows you a root like structure.

Again, combining this circle tree technique, I can now draw a circle trail to show the relationship between the circles!
I wrote some code to traverse my circle tree so that I could draw a pulsing trail.
It’s not obvious in this highly compressed gif, but I added some post processing — from within OpenRNDR itself — to lend some pizazz to the final output. Some bloom goes a long way!

Doing Poisson fill on it yields satisfyingly smooth gradients. Click the image to see the original one on Instagram as GIF compression kills it!
Other Techniques
Here are some other circular ideas I tried out.
Spirograph
Another idea that took me back to my primary school days was the spirograph. One of those mathematical drawing kits where you traced the path of a smaller circle rolling within a larger circle.

Fortunately for creative coders, we don’t have to simulate everything so that it represents physical reality! You can tweak how fast the inner circle rotates around its own center as well as how fast it rotates around the larger circle. Varying this yields different patterns. In fact, I made an interactive version where you can do exactly just that!
Physics

I have never really explored physics in creative coding before so I decided to try my hand at it!
What you see at your left is a bunch of circles whose radii vary over time. They are all trying to chase the moving dot but they get pushed around by each other as they do.
Doing this simulation, I noticed something. The circles naturally form some kind of local optimum for packing themselves, with the smaller circles always somewhat in the interior.
As usual, I always try to see if I can iterate an idea and combine techniques I’ve already developed. An interactive version of these can be found here.
“Always be iterating.”
Zach Lieberman’s 2017 Motto

Another physics technique was to use spring forces!
You can manually create a circle mesh and then connecting all the vertices with a spring.
By varying the spring’s stiffness and damping, you alter the behavior of the circle significantly.
For the interactive version, click here.
Vertex Transformations
This technique is a bit niche, but it’s based on the way the graphics card draws things on the screen — specifically, the way OpenGL draws things on the screen.
Without, getting too much into detail, you can feed OpenGL a bunch of vertices, tell it to draw a circle and it will draw a circle. But why do this manually when you can just circle() in any good creative coding framework?
The answer: vertex attributes.
Vertices aren’t just point on a screen. They contain data such as normals, texture coordinates and color. By manually feeding the data, you can get OpenGL to do stuff for you that normally would be too tedious to do yourself.
One such thing would be gradients!

The interactive version can be found here.
Webbing
Another reason to think in vertices is webbing!

By defining my circles as a set of vertices, I have access to these vertices. I can do maths over them. I can iterate over each vertice and check how close they are to the vertices of other circles. If they are near enough, I draw line.
Dubin Paths
Dubin paths are a specific kind of curve. Long story short, they can be defined with circles.

The algorithm for this is simple:
- Trace along the circumference of a circle
- At an arbitrary point, spawn a circle that is tangent to the current one
- Repeat
Summary
Thanks for reading this article all the way until the end! I hope some of these techniques inspired you somewhat. I encourage you to give it a go and try it out yourself. If you create something you feel worth sharing, reach out to me on Instagram or Twitter!
It can’t be said enough how important it is to iterate and look for combinations. There are quite a few artists doing daily art—Alexis Andre, Zach Lieberman, Saskia Freeke, Erika Anderson, Jason Ting, just to name a few — and they all do just that: iterate.